2015-2016 Petrozavodsk Winter Training Camp, Saratov SU Contest

发表于 2021-11-16

链接

A	B	C	D	E	F	G	H	I	J	K
$\color{green}{\texttt{+5}}$	$\color{red}{\texttt{+1}}$					$\color{green}{\texttt{+4}}$	$\color{green}{\texttt{+1}}$	$\color{green}{\texttt{+}}$	$\color{green}{\texttt{+}}$	$\color{red}{\texttt{+}}$

签到题。~~然而贡献了 4 发罚时~~。

考虑贪心，显然会选要求最低（深度最深）的若干个设备，同时插线板一定是越多口放越上面。

考虑二分答案，变成判定性问题。因为确定了深度最浅的设备，而插线板一定是能插就插不会更列，所以将当层设备插入之后剩下的口先贪心插接线板，如果没有了再插剩下的电器。

复杂度 $O(n\log n)$。

简化后题意就是给一个点集，问点 $(x,y)$ 与点集内点点积最小值。

直接建下凸包然后二分即可。复杂度 $O(n\log n)$。

赛时乱搞过了。考虑维护集合 $A,B$ 与 $B,C$ 的差值，直接 dp，可以做到 $O(n^3t^2)$，过不去。

考虑其实权值大于 $t^2$ 没有存的必要了。只取绝对值 $\leq t^2$ 的部分，复杂度 $O(nt^4)$。稍微卡卡常能过？

赛时直接取 $V=200$，然后 random_shuffle 过了。。。

如果 $i$ 存在一个后继是 $j$，事实上的限制只有 $a[i+1,j-1]$ 区间所有数与 $a_j$ 不同。

换句话说对于每个 $j$ 找到最小限制的 $l$，那么 $a_j=\operatorname{mex}_{k\in(l,j)}{a_k}$。

直接值域线段树。复杂度 $O(n\log n)$。

先枚举免费的路径的一个端点，考虑 dfs 过程中枚举另一个端点 $u$ 统计答案。可以发现直径只有：

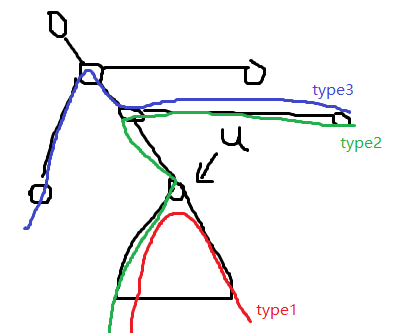
首先 dfs 一遍求出 $u$ 为根子树内最长链与一端为 $u$ 的最长链。

然后再 dfs 一遍，过程中传入一个点到根路径上的最长链与次长链。处理过程中可能会需要记录前三大值。最后分讨一下可以得到以 $u$ 为免费路径端点时的直径。

复杂度 $O(n^2)$。

假设右边第 $i$ 个点权值为 $2^i$，左边每个点权值 $v_i$ 为所有连出的边对应点权值异或和。

结论：以 $s$ 为当前点的游戏是先手必胜的当且仅当 $v_s$ 不能被 ${v_i},i\neq s$ 异或表示。

证明

构造 01 矩阵 $A$，$A_{i,j}=1$ 当且仅当左边的 $i$ 与右边的 $j$ 有边。

容易发现，结论转化为以 $s$ 为起点是先手必胜当且仅当 $A$ 的秩不等于 $A$ 删去第 $s$ 行的秩。

由于是平等博弈，所以先手移动到 $t$ 后是后手必败当且仅当 $A^T$ 删去第 $t$ 行后秩不发生变化。

由于 $A^T$ 的秩等于 $A$ 的秩，所以命题等价于：对于任意列 $s$，如果删去 $s$ 后秩变化，那么一定存在一个位置 $A_{s,i}=1$，满足将 $A_{s,i}$ 置 $0$ 后的秩等于删去第 $i$ 行后的秩。

因为删去 $s$ 后秩变化，所以 $s$ 必然存在一个主元行。容易证明将某个主元列的 $1$ 置 $0$ 后的秩等于删去该行后的秩。故命题得证。

然后直接暴力枚举哪一步可以使对方必败即可。