| A |
B |
C |
D |
E |
F |
| $\color{green}{\texttt{+3}}$ |
$\color{green}{\texttt{+}}$ |
$\color{green}{\texttt{+3}}$ |
$\color{green}{\texttt{+}}$ |
$\color{red}{\texttt{+5}}$ |
$\color{green}{\texttt{+}}$ |
A. Political Development
首先至少有一个点度数 $\leq k$,删去这个点后,同样至少有一个点度数 $\leq k$。
把与即将被删点相邻的至多 $k+1$ 个点拿出来跑一边最大独立集。复杂度 $O(nk2^k)$。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
| #include<iostream>
#include<cstdio>
#include<cstring>
#include<set>
#include<vector>
#define N 100010
using namespace std;
int deg[N];
set<pair<int,int>>s;
set<int>g[N];
int ans,as,f[20];
void solve(vector<int>&v)
{
int n=v.size();
for(int i=0;i<n;i++)
{
f[i]=0;
for(int j=0;j<n;j++)
if(i!=j && g[v[i]].count(v[j])) f[i]|=1<<j;
}
for(int s=1;s<1<<n;s++)
{
bool can=true;
for(int i=0;i<n && can;i++) if(s>>i&1 && (f[i]&s)!=(s^(1<<i))) can=false;
if(can) ans=max(ans,__builtin_popcount(s));
}
}
bool vis[N];
int main()
{
int n,k;scanf("%d%d",&n,&k);
for(int i=0;i<n;i++)
{
int x,y;scanf("%d",&x);deg[i]=x;
while(x --> 0) scanf("%d",&y),g[i].insert(y);
}
for(int i=0;i<n;i++) s.emplace(deg[i],i);
while(!s.empty())
{
int u=s.begin()->second;s.erase(s.begin());
vis[u]=true;
vector<int>p;p.push_back(u);
for(int v:g[u]) if(!vis[v]) p.push_back(v);
solve(p);
for(int v:p) if(!vis[v]) s.erase({deg[v],v}),s.emplace(--deg[v],v);
}
printf("%d\n",ans);
return 0;
}
|
B. Railway
用类似于虚树的想法,把每次要求的点按 dfn 排序,那么每个点贡献的边就是该点到该点和上一个点的 lca 部分。
直接离线后 dfs 一遍即可。
复杂度 $O(n\log n)$。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
| #include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
#include<map>
#include<algorithm>
#define N 100010
using namespace std;
vector<int>g[N];
int dep[N],siz[N],son[N],fa[N];
map<pair<int,int>,int>mp;
void dfs(int u,int p)
{
siz[u]=1;dep[u]=dep[p]+1;fa[u]=p;
for(int v:g[u]) if(v!=p)
{
dfs(v,u);siz[u]+=siz[v];
if(siz[v]>siz[son[u]]) son[u]=v;
}
}
int top[N],dfn[N],idx;
void dfs2(int u,int topp)
{
top[u]=topp;dfn[u]=++idx;
if(son[u]) dfs2(son[u],topp);
for(int v:g[u]) if(v!=fa[u] && v!=son[u]) dfs2(v,v);
}
int lca(int x,int y)
{
for(;top[x]!=top[y];x=fa[top[x]]) if(dep[top[x]]<dep[top[y]]) swap(x,y);
return dep[x]<dep[y]?x:y;
}
int w[N],ans[N],p[N];
void dfs3(int u){for(int v:g[u]) if(v!=fa[u]) dfs3(v),w[u]+=w[v];}
int main()
{
int n,m,k;scanf("%d%d%d",&n,&m,&k);
for(int i=1,u,v;i<n;i++) scanf("%d%d",&u,&v),g[u].push_back(v),g[v].push_back(u),mp[{u,v}]=mp[{v,u}]=i;
dfs(1,0);dfs2(1,1);
for(int i=1;i<=m;i++)
{
int q;scanf("%d",&q);
for(int i=1;i<=q;i++) scanf("%d",&p[i]);
sort(p+1,p+q+1,[&](int x,int y){return dfn[x]<dfn[y];});
w[p[1]]++;int l=p[1];
for(int i=2;i<=q;i++) w[p[i]]++,w[lca(p[i],p[i-1])]--,l=lca(l,p[i]);
w[l]--;
}
dfs3(1);
for(int i=2;i<=n;i++) ans[mp[{fa[i],i}]]=w[i]>=k;
int tt=0;
for(int i=1;i<n;i++) tt+=ans[i];
printf("%d\n",tt);
for(int i=1;i<n;i++) if(ans[i]) printf("%d ",i);
return 0;
}
|
C. Toll
观察到题目给的其实是一个分层图,且每层至多 $k$ 个点,$k\leq 5$。
直接用 $f_{i,x,y}$ 表示第 $i$ 层的 $x$ 到 $i+1$ 层的 $y$ 的最短距离,这显然可以写成 $\max$ 矩阵的形式。题意等同于问区间矩阵乘积,可以直接分治解决,复杂度 $O(nk^3\log q)$,常数极小。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
| #include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
#define N 100010
#define M 5
#define fi first
#define se second
using namespace std;
int n,m,k,q;
struct matr{
int a[M][M];
matr(){memset(a,0x3f,sizeof(a));}
int* operator [](int x){return a[x];}
}g[N],p[N];
matr operator *(matr x,matr y)
{
matr z;
for(int i=0;i<k;i++)
for(int t=0;t<k;t++)
for(int j=0;j<k;j++) z[i][j]=min(z[i][j],x[i][t]+y[t][j]);
return z;
}
struct node{
int l,lx,r,rx,t;
};
int ans[N];
void solve(int l,int r,vector<node> &Q)
{
if(l==r)
{
for(auto x:Q) if(x.l==x.r) ans[x.t]=g[x.l][x.lx][x.rx];
return;
}
if(Q.empty()) return;
int mid=(l+r)>>1,fl=mid,fr=mid+1;
vector<node> ql,qr;
for(auto x:Q) if(x.l<=mid && mid<x.r) fl=min(fl,x.l),fr=max(fr,x.r);
p[mid]=g[mid];for(int i=mid-1;i>=fl;i--) p[i]=g[i]*p[i+1];
p[mid+1]=g[mid+1];for(int i=mid+2;i<=fr;i++) p[i]=p[i-1]*g[i];
for(auto x:Q) if(x.l<=mid && mid<x.r)
ans[x.t]=(p[x.l]*p[x.r])[x.lx][x.rx];
else if(x.r<=mid) ql.push_back(x);else if(x.l>mid) qr.push_back(x);
solve(l,mid,ql);solve(mid+1,r,qr);
}
int main()
{
scanf("%d%d%d%d",&k,&n,&m,&q);
int mx=(n+k-1)/k;
for(int i=1,u,v,w;i<=m;i++) scanf("%d%d%d",&u,&v,&w),g[u/k][u%k][v%k]=w;
vector<node>Q;
for(int i=0,x,y;i<q;i++) scanf("%d%d",&x,&y),Q.push_back({x/k,x%k,y/k-1,y%k,i});
memset(ans,-1,sizeof(ans));
solve(0,mx-1,Q);
for(int i=0;i<q;i++) printf("%d\n",ans[i]>=1e9?-1:ans[i]);
return 0;
}
|
D. Cat in a tree
一开始想了一个反悔堆贪心,后来发现完全没有必要。
首先反悔堆贪心比较显然:用小根堆记录每个子树里面选的深度,每次合并的时候判断两个堆顶是否不合法,如果不合法贪心删去较浅的那一个,容易证明是正确的。
然而事实上一个堆只会被至多弹依次。如果一个子树中 $a,b$ 被选择了,另一个子树中 $c,d$ 被选择了,要想某个堆弹出两次,需要 $\text{dis}(a,c)< m,\text{dis}(b,d)< m$,然而 $\text{dis(a,b)}+\text{dis}(c,d)<\text{dis}(a,c)+\text{dis}(b,d)$,故 $\text{dis}(a,c)+\text{dis}(b,d)> 2m$。所以一个堆至多被弹一次。
那么只需要记录一个点子树内最浅的位置,然后每次扫子树过程中发现不合法,就将最浅的位置删掉即可。
复杂度 $O(n)$。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| #include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
#include<algorithm>
#define N 200010
using namespace std;
int f[N],ans,m;
vector<int>g[N];
void dfs(int u,int p)
{
f[u]=m;
for(int v:g[u])
{
dfs(v,u);
if(f[u]+f[v]+1<m) --ans,f[u]=max(f[u],f[v]+1);
else f[u]=min(f[u],f[v]+1);
}
if(f[u]>=m) ++ans,f[u]=0;
}
int main()
{
int n;scanf("%d%d",&n,&m);
for(int i=2,u;i<=n;i++) scanf("%d",&u),g[u+1].push_back(i);
dfs(1,0);
printf("%d",ans);
return 0;
}
|
E. Friends
很妙的题。
考虑 $p+q$ 很小,采用暴力增广,即每次从一个点 $i$ 开始,暴力枚举其所有出边。如果某一时刻集合出边个数加上集合内点数超过 $p+q$ 直接无解。否则枚举每条出边是否塞进集合,总共只有 $2^{p+q}$ 种可能。
算出所有集合后考虑一个性质:如果 $A,B$ 都是合法集合,那么 $A\backslash B$ 和 $B\backslash A$ 中必然有一个是合法的。
考虑反证,显然点数不会不合法。假设分开集合为 $A,B$,公共部分为 $C$。
如果边数不合法,假设 $A$ 向 $B$ 连边为 $a$(粉色边),$A$ 向 $C$ 连边为 $b$(黄色边),$B$ 向 $C$ 连边为 $c$(蓝色边),$A,C,B$ 向外面连边为 $d,e,f$。
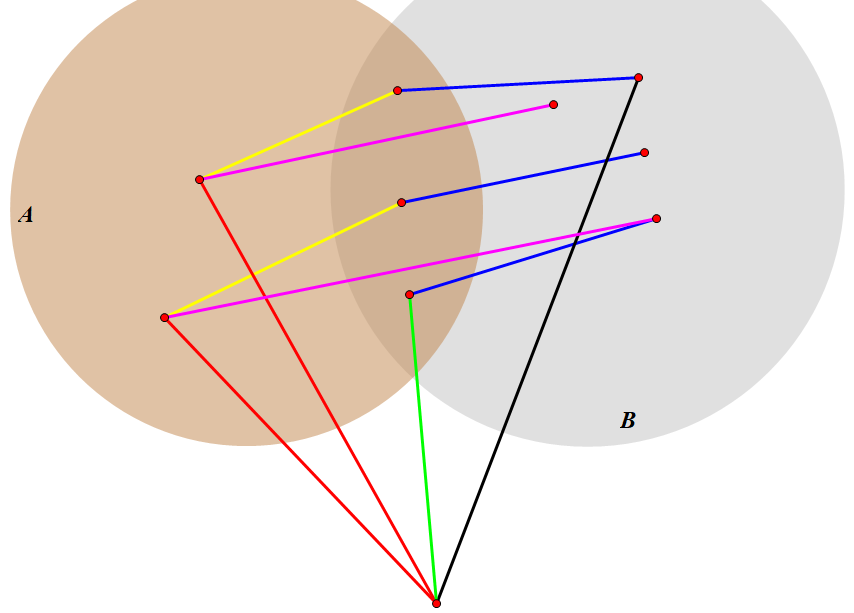
那么有 $a+b+d>q,a+c+f>q$,因为 $A,B$ 要合法,有 $a+c+d+e\leq q,a+b+e+f\leq q$,$2a+b+c+d+2e+f\leq 2q<2a+b+c+d+f$,推出 $e<0$,不合法。
所以只需要找出所有初始集合,然后调整即可。
复杂度 $O(n2^{p+q}+n^2p)$。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
| #include<iostream>
#include<cstdio>
#include<cstring>
#include<set>
#include<queue>
#define N 5100
using namespace std;
set<int>g[N];
int n,m1,m2;
bool check(const set<int>&s)
{
if(s.size()>m1) return false;
int tt=0;
for(int u:s)
{
if(g[u].size()>m1+m2) return false;
for(int v:g[u]) if(!s.count(v))
{
if(++tt>m2) return false;
}
}
return true;
}
bool vis[N];
set<int>f[N],s,t,o,tmp[N];
int tt;
bool solve()
{
if(s.size()>m1 || s.size()+t.size()+o.size()>m1+m2 || o.size()>m2) return false;
if(t.empty())
{
if(check(s))
{
for(int u:s) vis[u]=true;
f[++tt]=s;
return true;
}
return false;
}
int u=*t.begin();
tmp[u]=t;t.erase(u);
if(!s.empty())
{
o.insert(u);
if(solve()) return true;
o.erase(u);
}
s.insert(u);
for(int v:g[u]) if(!s.count(v) && !t.count(v) && !o.count(v)){t.insert(v);if(s.size()+t.size()>m1+m2) break;}
if(solve()) return true;
s.erase(u);
t=tmp[u];
return false;
}
void adjust(int x,int y)
{
bool hv=true;
for(int v:f[x]) if(f[y].count(v)){hv=false;break;}
if(hv) return;
set<int>z=f[x];
for(int v:f[y]) if(z.count(v)) z.erase(v);
if(check(z)){f[x]=z;return;}
z=f[y];
for(int v:f[x]) if(z.count(v)) z.erase(v);
if(check(z)){f[y]=z;return;}
throw;
}
set<set<int>>ans;
int main()
{
scanf("%d%d%d",&n,&m1,&m2);
for(int i=1;i<=n;i++)
{
int k;scanf("%d",&k);
for(int j=1,x;j<=k;j++) scanf("%d",&x),g[i].insert(++x);
}
for(int i=1;i<=n;i++)
for(int v:g[i]) if(!g[v].count(i)){puts("detention");return 0;}
for(int i=1;i<=n;i++)
if(!vis[i])
{
s=o={},t={i};
if(!solve()){puts("detention");return 0;}
}
puts("home");
for(int i=1;i<=tt;i++)
for(int j=i+1;j<=tt;j++) adjust(i,j);
for(int i=1;i<=tt;i++) if(!f[i].empty()) ans.insert(f[i]);
printf("%d\n",(int)ans.size());
for(auto &s:ans)
{
printf("%d ",(int)s.size());
for(int u:s) printf("%d ",u-1);
puts("");
}
return 0;
}
|
F. Plus Minus
签到题,可以发现要么行 $+/-$ 交替,要么列 $+/-$ 交替,最后减去重复部分(行列都 $+/-$ 交替)即可。
算出每种情况可以自由选择的个数 $v$,那么贡献就是 $2^v$。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| #include<iostream>
#include<cstdio>
#include<cstring>
#include<map>
#define N 100010
#define mod 1000000007
using namespace std;
int x[N],y[N],op[N];char s[3];
int ksm(int a,int b=mod-2)
{
if(b<0) return 0;
int r=1;
for(;b;b>>=1,a=1ll*a*a%mod) if(b&1) r=1ll*r*a%mod;
return r;
}
map<int,int>mp;
int main()
{
int n,m,k;scanf("%d%d%d",&n,&m,&k);
if(k==0){printf("%d",(ksm(2,n)+ksm(2,m)-2)%mod);return 0;}
for(int i=1;i<=k;i++) scanf("%s%d%d",s,&x[i],&y[i]),op[i]=s[0]=='+';
int tt=n;
for(int i=1;i<=k;i++)
if(!mp.count(x[i])) mp[x[i]]=(y[i]^op[i])&1,tt--;
else if(mp[x[i]]!=((y[i]^op[i])&1)){tt=-1;break;}
int ans=ksm(2,tt);
tt=m;
mp.clear();
for(int i=1;i<=k;i++)
if(!mp.count(y[i])) mp[y[i]]=(x[i]^op[i])&1,tt--;
else if(mp[y[i]]!=((x[i]^op[i])&1)){tt=-1;break;}
ans=(ans+ksm(2,tt))%mod;
int al=(x[1]+y[1]+op[1])&1,c=1;
for(int i=2;i<=k;i++) if(al!=((x[i]+y[i]+op[i])&1)){c=0;break;}
ans=(ans-c+mod)%mod;
printf("%d\n",ans);
return 0;
}
|
