Baltic Olympiad in Informatics 2019

发表于
Flash Nautilus Valley Kitchen Necklace Olympiads
$\color{green}{\texttt{-}}$ $\color{green}{\texttt{+}}$ $\color{green}{\texttt{+}}$ $\color{green}{\texttt{+1}}$ $\color{green}{\texttt{+1}}$ $\color{red}{\texttt{+2}}$

链接 题面链接 中文题面

B. Nautilus

考虑用 $f_{i,j,t}$ 表示点 $(i,j)$ 是否可能在 $t$ 时间被到达。显然可以 $O(1)$ 转移。

注意到转移都是或操作，直接 bitset 优化。复杂度 $O(\frac{n^2m}{\omega})$。

代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include<iostream>
#include<cstdio>
#include<cstring>
#include<bitset>
#define N 502
#define M 5010
using namespace std;
bitset<N>f[N],g[N],mp[N];
char s[M];
int main()
{
    int n,m,k;scanf("%d%d%d",&n,&m,&k);
    for(int i=1;i<=n;i++)
    {
        scanf("%s",s+1);
        for(int j=1;j<=m;j++) if(s[j]=='.') mp[i].set(j);
    }
    for(int i=1;i<=n;i++) f[i]=mp[i];
    scanf("%s",s+1);
    for(int i=1;i<=k;i++)
    {
        for(int i=1;i<=n;i++) g[i]=f[i],f[i].reset();
        if(s[i]=='N' || s[i]=='?') for(int i=1;i<=n;i++) f[i]|=g[i+1];
        if(s[i]=='S' || s[i]=='?') for(int i=1;i<=n;i++) f[i]|=g[i-1];
        if(s[i]=='W' || s[i]=='?') for(int i=1;i<=n;i++) f[i]|=g[i]>>1;
        if(s[i]=='E' || s[i]=='?') for(int i=1;i<=n;i++) f[i]|=g[i]<<1;
        for(int i=1;i<=n;i++) f[i]&=mp[i];
    }
    int ans=0;
    for(int i=1;i<=n;i++) ans+=f[i].count();
    printf("%d\n",ans);
    return 0;
}

C. Valley

题面给了一个点 $E$，换句话说如果断边不在 $u$ 到 $E$ 路径上直接输 escaped。

如果以 $E$ 为根，实际上断边等价于取一个子树。换句话说，如果父亲可达，那么其子树都可达。

考虑倍增，因为 $\text{dis}(x,y)=\text{dep}(x)+\text{dep}(y)-2\text{dep}(\operatorname{lca}(x,y))$，假设 $\text{lca}(x,y)$ 在 $y$ 向上 $2^i$ 的父亲中，取 $\min$ 即可。

最后查询倍增。复杂度 $O((n+q)\log n)$。

代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
#include<algorithm>
#define N 100010
#define ll long long
#define inf 10000000000000000
using namespace std;
int nxt[N<<1],to[N<<1],w[N<<1],head[N],cnt;
void add(int u,int v,int w0){nxt[++cnt]=head[u];to[cnt]=v;w[cnt]=w0;head[u]=cnt;}
int dfn[N],fa[N],siz[N],idx;
ll dis[N];int rid[N];
void dfs1(int u,int p)
{
    dfn[u]=++idx;siz[u]=1,fa[u]=p;
    for(int i=head[u];i;i=nxt[i])
    {
        int v=to[i];if(v==p) continue;
        dis[v]=dis[u]+w[i];rid[(i+1)/2]=v;
        dfs1(v,u);siz[u]+=siz[v];
    }
}
bool col[N];ll h[N],f[N][22],g[N][22];
void dfs2(int u)
{
    h[u]=col[u]?0:inf;
    for(int i=head[u];i;i=nxt[i]) if(to[i]!=fa[u]) dfs2(to[i]),h[u]=min(h[u],h[to[i]]+w[i]);
}
int rt,n;
void init()
{
    for(int i=1;i<=n;i++) g[i][0]=h[i]-dis[i],f[i][0]=fa[i];
    for(int d=1;1<<d<=n;d++)
        for(int i=1;i<=n;i++) g[i][d]=min(g[i][d-1],g[f[i][d-1]][d-1]),f[i][d]=f[f[i][d-1]][d-1];
}
int main()
{
    int s,q;scanf("%d%d%d%d",&n,&s,&q,&rt);
    for(int i=1,u,v,w;i<n;i++) scanf("%d%d%d",&u,&v,&w),add(u,v,w),add(v,u,w);
    dfs1(rt,0);
    for(int i=1,x;i<=s;i++) scanf("%d",&x),col[x]=true;
    dfs2(rt);init();
    while(q --> 0)
    {
        int u,d;scanf("%d%d",&d,&u);
        d=rid[d];
        if(dfn[d]>dfn[u] || dfn[d]+siz[d]<=dfn[u]){puts("escaped");continue;}
        ll res=inf,ex=dis[u];
        for(int i=20;i>=0;i--) if(dis[f[u][i]]>=dis[d]) res=min(res,g[u][i]),u=f[u][i];
        res=min(res,g[u][0]);
        if(res>=1e15){puts("oo");continue;}
        printf("%lld\n",res+ex);
    }
    return 0;
}

D. Kitchen

显然一个必要条件是 $\sum a_i\geq \sum b_i$ 且 $b_i\geq k$。

在这个条件下，我们可以先让每个厨师参与尽可能多的菜，最后再单独做。这样匹配就变成：左边每个点可以匹配 $a_i$ 个，右边强制匹配 $k$ 个，问是否合法。

由于 $\sum a_i\geq\sum b_i\geq nk$，上面的强制匹配可以看做是最大匹配为 $nk$。这是 Hall 定理的一个经典结论：最大匹配成立当且仅当 $\sum \max(a_i,n)\geq nk$。

用 $f_{i,j}$ 表示前 $i$ 个厨师，$\sum a_i$ 为 $j$ 时 $\sum \max(a_i,n)$ 的最大值。然后枚举所有 $\geq \sum b_i$ 且合法中最小的即可。复杂度 $O(n^3)$。

代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include<iostream>
#include<cstdio>
#include<cstring>
#define N 310
using namespace std;
int f[N*N],g[N*N];
int a[N],b[N];
int main()
{
    int n,m,k;scanf("%d%d%d",&n,&m,&k);
    int sa=0,sb=0;
    for(int i=1;i<=n;i++) scanf("%d",&a[i]),sa+=a[i];
    for(int i=1;i<=m;i++) scanf("%d",&b[i]),sb+=b[i];
    if(sa>sb){puts("Impossible");return 0;}
    for(int i=1;i<=n;i++) if(a[i]<k){puts("Impossible");return 0;}
    memset(g,0xcf,sizeof(g));
    g[0]=0;sb=0;
    for(int i=1;i<=m;i++)
    {
        memcpy(f,g,sizeof(f));
        for(int j=0;j<=sb;j++)
            g[j+b[i]]=max(g[j+b[i]],f[j]+min(b[i],n));
        sb+=b[i];
    }
    for(int i=sa;i<=sb;i++)
        if(g[i]>=n*k){printf("%d\n",i-sa);return 0;}
    puts("Impossible");
    return 0;
}

E. Necklace

首先翻转可以直接将正串和反串分别匹配，可以不考虑。

重点在于串可以循环同构，不太好处理。不妨假设一个串可以表示为 $L+R$，另一个串表示为 $R+L$。考虑枚举两个串中的分界点 $p_1,p_2$：

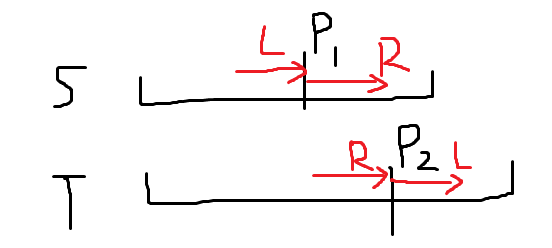
image

直接枚举 $p_1,p_2$，Hash 判断 $L,R$ 是否合法，复杂度 $O(n^3)$。

考虑优化。不妨将 $S$ 和 $T$ 链接起来，中间放置一个特殊字符：

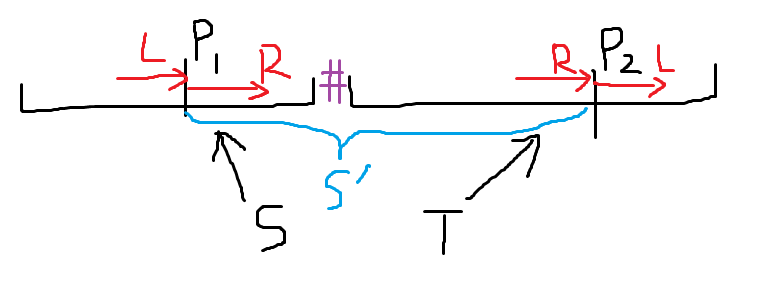
image

取 $p_1,p_2$ 中间的串 $S’$，可以发现 $R$ 就是 $S’$ 的 border。而枚举 $p_1$，所有 $p_2$ 的 border 可以在 $O(n)$ 时间算出。

同样将 $S$ 和 $T$ 翻转后拼接就可以得到 $R$。所以枚举 $p_1$，可以在 $O(n)$ 时间得到每个位置的 $L,R$ 长度，最后扫一遍更新答案即可。

复杂度 $O(n^2)$。

代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define N 6010
using namespace std;
char s[N],t[N],tmp[N];
int n,m,q;
int nxt[N],f[N],g[N];
void get_nxt()
{
    // printf("get %s :",tmp+1);
    int p=0;
    for(int i=2;i<=q;i++)
    {
        while(p && tmp[p+1]!=tmp[i]) p=nxt[p];
        if(tmp[p+1]==tmp[i]) ++p;
        nxt[i]=p;
    }
    // for(int i=1;i<=q;i++) printf("%d ",nxt[i]);puts("");
}
void putl(int p)
{
    q=0;
    for(int i=p;i<=n;i++) tmp[++q]=s[i];
    tmp[++q]='$';int l=q;
    for(int i=1;i<=m;i++) tmp[++q]=t[i];
    get_nxt();
    for(int i=1;i<=m;i++) f[i]=nxt[i+l];
}
void putr(int p)
{
    q=0;
    for(int i=p;i;i--) tmp[++q]=s[i];
    tmp[++q]='$';int l=q;
    for(int i=m;i;i--) tmp[++q]=t[i];
    get_nxt();
    for(int i=1;i<=m;i++) g[m-i+1]=nxt[i+l];
}
int ans=0,sl,tl;
void solve()
{
    for(int p=1;p<=n;p++)//在 p 位置断开
    {
        putl(p);putr(p-1);
        // printf("%d\n",p);
        // for(int i=1;i<=n;i++) printf("%d ",f[i]);puts("");
        // for(int i=1;i<=n;i++) printf("%d ",g[i]);puts("");
        for(int i=1;i<=m+1;i++)
        if(f[i-1]+g[i]>ans)
        {
            ans=f[i-1]+g[i];
            sl=p-g[i];tl=i-f[i-1];
        }
    }
}
int main()
{
    scanf("%s%s",s+1,t+1);
    n=strlen(s+1),m=strlen(t+1);
    solve();
    reverse(s+1,s+n+1);sl=n-(sl+ans-1)+1;
    solve();sl=n-(sl+ans-1)+1;
    printf("%d\n%d %d\n",ans,sl-1,tl-1);
    return 0;
}

F. Olympiads

很常见的套路。考虑一般的类似 $k$ 短路问题有两个方向，一个是 A* 乱搞，这里考虑另一种：

  • 首先求出所有可能方案中最大的那一个。在这道题里就是依次取每个项目中没有被选的人中最大的。
  • 增广所有可能的次大值。可以发现如果指定前 $k$ 个位置，后面要最大同样会取没有被选的人中最大的。可以枚举 $k$，将 $k$ 取次大值，然后 $k+1\sim n$ 取最大值。
  • 保证增广唯一。这个比较繁琐，因为事实上 ${1,2,3}$ 和 ${2,3,1}$ 应该是等价的。
    题解有一个比较好的实现方式，具体来说可以发现所有重复部分源于一个人 $u$ 如果被指定替换成另一个人 $v$ 之后，$u$ 又在后面出现了。
    所以我们钦定一个人如果被指定替换，那么他就不应该在后续出现。那么额外存一个集合表示仍然可以出现的人即可。

最后只要依次取出优先队列中的元素，然后增广即可。

分析复杂度，一次增广会 push $O(k)$ 个元素，处理一个元素需要 $O(nk)$ 的时间，总增广次数 $O(c)$，所以总复杂度 $O(nk^2c+ck\log n)$。

代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include<iostream>
#include<cstdio>
#include<cstring>
#include<bitset>
#include<algorithm>
#include<queue>
#include<set>
#define N 510
#define M 2010
#define K 7
#define fi first
#define se second
using namespace std;
int n,m;
int w[N][K];pair<int,int>a[K][N];
struct node{
    int v,chs[K],las;bitset<N>vis;
    node(){v=las=0;memset(chs,0,sizeof(chs));vis.reset();}
    bool operator <(const node a)const{return v<a.v;}
    void init()
    {
        v=0;
        for(int i=1;i<=m;i++){int r=0; for(int j=1;j<=m;j++) r=max(r,w[chs[j]][i]); v+=r;}
    }
};
node get_next(const node &u,int l)
{
    node v=u;
    for(int k=l+1;k<=m;k++) v.vis[v.chs[k]]=false,v.chs[k]=0;
    for(int k=l;k<=m;k++)
        for(int i=1;i<=n;i++) if(!v.vis[a[k][i].se]){v.chs[k]=a[k][i].se;v.vis[a[k][i].se]=1;break;}
    v.las=l; v.init();return v;
}
node fir(){node u;return get_next(u,1);}
priority_queue<node>q;
int main()
{
    int k=0;
    scanf("%d%d%d",&n,&m,&k);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++) scanf("%d",&w[i][j]),a[j][i]={w[i][j],i};
    for(int i=1;i<=m;i++) sort(a[i]+1,a[i]+n+1,greater<pair<int,int>>());
    q.push(fir());
    while(k --> 1)
    {
        node u=q.top();q.pop();
        if(u.vis.count()==n) continue;
        for(int i=u.las;i<=m;i++) q.push(get_next(u,i));
    }
    printf("%d\n",q.top().v);
    return 0;
}